『知識と感情を融合させた表現が出来るギタリスト』になる為の Intelligence & Emotional Guitar

さて、続いてKeyについてやっていきましょう。

 

 

前回、Keyの判別法は二つある、ということを書きました。

 

 

その二つの判別法とは、

 

１、楽譜の調号をみる

 

２、コード進行から読みとる

 

の、ことでしたね。

 

 

で、実際の楽譜上で、

 

・調号とはどれのことを言うのか？

 

・調号は楽譜のどこに表記されるのか？

 

を解説しました。

 

 

今回は、

実際に調号からKeyをどうやって判別するのか？

そのやりかたを覚えましょう。

 

 

ではまず、以下の図を見てください。

 

図１

 

 

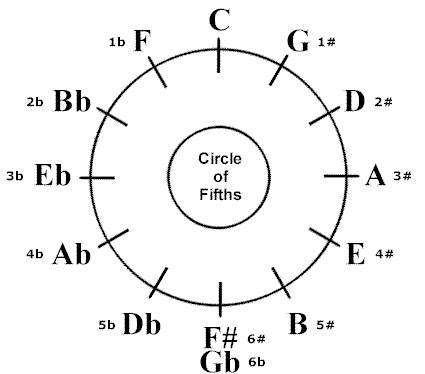
この図は、

サークルオブフィフス(Circle Of Fifths)

といいます。

 

 

他にサイクル・オブ・フィフス(Cyle Of Fifths)や、
日本語で五度圏(ごどけん)と呼ばれたりもします。

 

 

どの呼び方で呼ばれても全て同じものを指します。

 

 

音楽理論の多くのコトをわかりやすーく表した図なので、ちょー便利です。

 

 

印刷して壁に貼っておきましょう笑

 

 

今回はKeyのお話なので、図1の英文字は、Keyのトニックを
指している、と思ってください。

 

 

もう一度見てみましょうか。

 

各英文字の横に、#もしくは♭と、数字が記されてありますね？

 

 

これは、

 

そのKeyの時、
#もしくは♭が数字の数だけ
調号として五線譜に表記される、

 

ということを表しています。

 

 

例を挙げると、

 

Key=Gなら、1#と記されているので、
#が一つ譜面に付きます。

 

Key=G時の調号

 

Key=E♭ならフラットが3つ。

 

Key=E♭時の調号

 

Key=Bなら#が5つ。

 

Key=B時の調号

 

ちゃんと数字どおりに調号が付いています。

 

 

ここで二点、疑問が浮かびます。

 

それは、

 

１、なぜ、そのKeyだと、調号がその数だけ付くのか？

２、なぜ、その順番で音に#や♭が付くのか？

 

ということです。

 

 

これにはちゃんと理由があります。

 

 

ではまず、1の、

 

なぜ、そのKeyだと、調号がその数だけ付くのか？

 

から解説していきましょう。

 

 

以前の記事で、メジャースケールとは、

 

ルート(一音目)→全音→全音→半音→全音→全音→全音→半音

 

という、ルート音からの音の並び(音階)だということを解説しました。

 

 

では、上に例を載せた、Key=Gで考えてみましょう。

 

3弦上で見た場合のGメジャースケール指板図

 

 

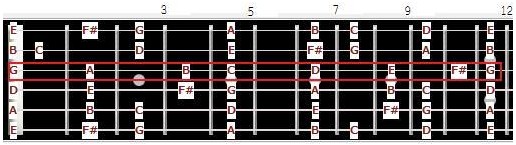
トニックをG音にして、メジャースケールのインターバルに当てはめてみると、

 

G(ソ)→全音→A(ラ)→全音→B(シ)→半音→C(ド)→
全音→D(レ)→全音→E(ミ)→全音→F#(ファ#)→半音→G

 

と、なって、

 

Cメジャースケールとの違いは、
F(ファ)がF#(ファ#)になっている所です。

 

 

譜例１、Gメジャースケール

 

音符の方を見ると、ちゃんとF(ファ)に#が付いて、
F#(ファ#)になっていますね。

 

 

Key解説その3で、

 

その曲のKeyのトニック
＝その曲を構成しているスケールのトニックである

 

ということを学びましたね。

 

ということは、
Key=Gの曲で使われるスケールは、
基本的にはGメジャースケールだってことです。

 

 

Gメジャースケールは、F(ファ)がF#(ファ#)になります。

 

 

KeyがGの間は、基本的には曲中ずっとF#(ファ#)です。

 

 

基本的に曲中ずっとF#なら、譜面の最初に指定してしまったほうが、
読みやすいよね、ってことで、譜面の頭に調号をつけます。

 

で、こうなるワケです。

 

Key=G時の調号

 

これなら、演奏者は、最初に譜面を見た時点で、
Key＝Gであることが一目でわかります。

 

あと最初にFが#することを指定しているので、
F音の位置に音符が出てきたらF#を弾くことになります。

 

譜例2、Key=G表記時のGメジャースケール

 

譜例１と見比べてみましょう。

 

譜例1

 

譜例２では、ちゃんと最初にF(ファ)に#が付いていますね？

 

 

最初に調号をつけておかないと、

Fの音符が出てくるたびに音符に#をつけなくてはならず、
超まぎらわしいのです。

 

 

♭の付き方も一緒です。

 

 

コレも上の例に挙げたKey=E♭で考えてみましょう。

 

 

E♭メジャースケールの構成音は、

 

E♭、F、G、A♭、B♭、C、D

 

になります。

 

E、A、B音に♭が付いていますね？

 

コレを調号で表記するとこうなります。

 

Key=E♭時のE♭メジャースケール

 

概要はGメジャースケールの解説と一緒です。

 

以上が、

 

なぜ、そのKeyだと、調号がその数だけ付くのか？

 

の理由になります。

 

 

要するに、

 

Keyが決まると、楽曲を主に構成するスケールが決まるので、
そのスケールに付く、#や♭を、譜面の最初に表記してしまおう、

 

って事です。

 

 

で、それによって、譜面内の音符に、わざわざ#や♭をつけなくて済むので、
譜面がスッキリして読みやすくなります。

 

 

演奏者が、曲のKeyがなんなのか、最初に把握できるようにもなりますね。

 

 

2つ目の疑問、

 

なぜ、その順番で音に#や♭が付くのか？

 

は次回です。

 

おそらく、今回の記事は、このブログ内で最長だと思うので、
じっくり読んで理解してください笑

 

 

では次回に続きます！

 

shun